Key Points
- Lamb shift arises from electron transitions affected by vacuum interactions.
- Researchers calculated “two-loop” self-energy corrections with unprecedented precision.
- The work refined the Rydberg constant’s precision to one part in a trillion.
- Methodology impacts experiments like Fermilab’s Muon g-2 study. Findings bolster QED’s predictive power and role in physics beyond the Standard Model.
The Lamb shift, a pivotal phenomenon in quantum electrodynamics (QED), has long been a challenging benchmark for physicists. First observed by Willis Lamb and Robert Retherford in 1947, the Lamb shift represents a subtle energy difference arising from the electron’s transition between hydrogen’s 2P1/2 and 2S1/2 energy levels. This transition defied conventional quantum mechanics and Dirac’s relativistic equation, stemming from vacuum interactions absent in earlier models.
As QED evolved, calculating the Lamb shift became crucial for addressing theoretical complexities like divergent integrals and singularities. Physicists have refined the fine-structure constant’s measurement by accurately predicting the shift to an uncertainty of less than one part in a million. On this foundation, scientists from the Max Planck Institute for Nuclear Physics in Germany, led by Vladimir Yerokhin, have achieved a groundbreaking advancement.
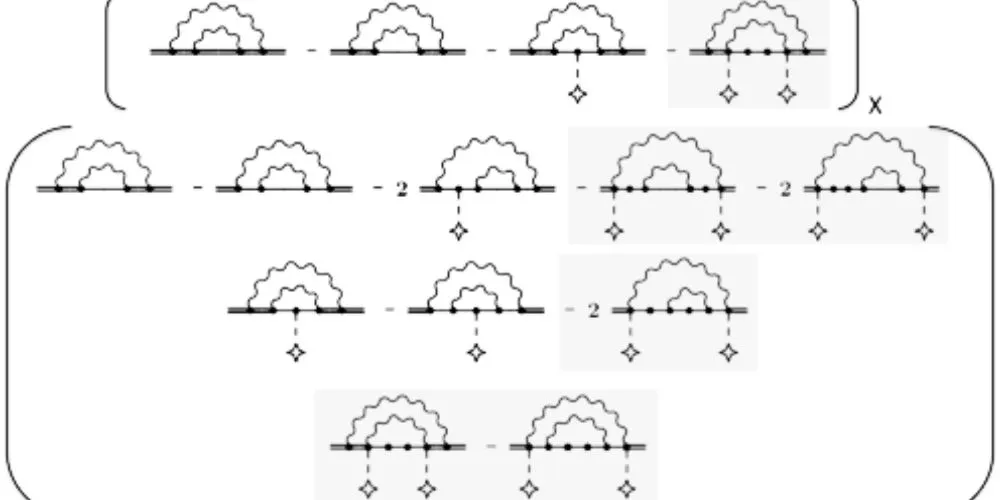
Their work, recently published in Physical Review Letters, focuses on the “two-loop” electron self-energy—a critical yet computationally formidable component of the Lamb shift. This self-energy describes changes in an electron’s energy caused by its interactions with its environment. Utilizing Feynman diagrams, the team modeled this quantum process involving two virtual photons emerging from the vacuum, influencing the 1S electron state.
Yerokhin and his colleagues enhanced numerical precision, calculating two-loop corrections to all orders of the parameter Zα, which encapsulates nuclear interactions. This improvement reduced the theoretical uncertainty of the 1S–2S Lamb shift in hydrogen and refined the Rydberg constant by one part in a trillion, advancing its precision beyond prior limitations.
Their methodology extends to QED phenomena, including corrections to the anomalous magnetic moments or g-factors of electrons and muons. This has direct implications for ongoing experiments like the Muon g-2 study at Fermilab, which explores potential deviations from the Standard Model. This research strengthens QED’s theoretical foundation by improving computational accuracy and broadening the scope of calculations. It also opens avenues for future discoveries in fundamental physics.